Why you should wait to teach projectile motion part 2: introducing projectile motion using Angry Birds

This is part 2 in a 3 part series about how I’ve decided to move teaching projectile motion from one of the earliest units I teach, until after my students have a thorough grounding in vectors, Newton’s laws and momentum. In part 1, I discussed the problem I see with teaching projectile motion as one of the earliest units in physics (before Newton’s Laws).

Introducing projectile motion with Angry Birds

As I wrote previously, projectile motion really is a wonderful topic to study for students. The ideas motion of footballs, golf balls, and astronauts all, on a fundamental level, are controlled by the same single force, and their motion evolves in the same predictable way is very powerful. Matt Ridley recently wrote a beautiful article exploring how this motion, and or passion for games involving predicting where a projectile with a parabolic trajectory will land is deeply tied to our own evolution. This article served as a wonderful motivator for why my students should study projectile motion.

Inspired by Rhett Allain and his exploration of Angry Birds, I thought the best way to study projectile motion would be to begin by checking out the laws of physics on Angry Bird world.

a vector construction of change in velocity for a small part of the angry bird's trajectory;

This was enough for students to catch on and realize there must be a downward force (they wondered if it was the gravitational force) in the Angry Bird world, but since it was a pretty qualitative sketch, you couldn’t conclude for sure that there is no air resistance on AB world. You’d need to do something more quantitative to see that.

So how can we get more quantitative? My students instantly thought of Video Physics, which is a wonderful app, but I wanted to show them something even more powerful, Tracker Video Analysis. By far the most tedious part of any video analysis is having to click and mark the object of interest in individual frames. Doing this for much more than a few seconds turns into a true exercise in tedium. Enter Tracker, and it’s incredible autotracker. Here’s another wonderful chance to talk about computational thinking.

me: do you find it tedious to mark the location of the angry bird on 100 different frames?
s: yes!
me: Why?
s: because it’s dull, mindless and repetitive!
me: Dull, mindless and repetitive—that’s like the “beetlejuice, beetlejuice beetlejuice” of computers. A computer should be able to do this for you, and you need recognize these moments and call for computer reinforcements.
s: So, you can essentially say, hey computer find the angry bird in every frame and mark it?
me: yes. When would this fail?
s: When it’s hard to tell the angry bird from it’s surroundings?
me: when would that be?
s: when there isn’t enough contrast between the bird and the surroundings? Or when the bird changes shape?
me: bingo.

And so here’s the autotracker in action. IMO, this feature takes video analysis from the “fun and useful for people who know what they’re doing”, to “everybody should give this a whirl” category.

When I then showed them the projection of the the “trajectory of the angry brid, students were puzzled, but pretty quickly someone realized that the background is moving, and we need to account for that in order to properly track the bird’s motion.

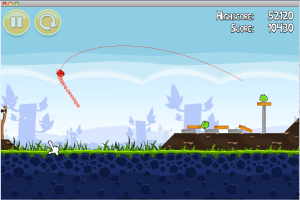
because the background moves in the film, the trajectory of the bird recorded by tracker isn't the actual trajectory.

So we need something that stands still, and is visible for the whole time to serve as an origin. The pig will do nicely. Autotracker again, and we can plot the position of the bird relative to the pig.

My students really don’t jump for equations nearly as much as students I taught in previous years before I used the modeling curriculum. Instead, they think of models—whole collections of ideas (diagrams, graphs, equations and explanations) that can be used to to explain a phenomena. This really is a huge shift, and it gives my students much more power over thinking about physical situations and problem solving.

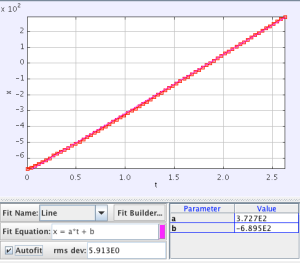
I decide to put this to the test by having them look at some data. I ask the students what to look at and they say the horizontal
position. Here we go:

The horizontal position of the Angry Bird, relative to the green pig.

What does this look like? What models accurately describe this motion? My students easily see this is a case of constant velocity (CVPM), and that the net force in the horizontal direction must be zero (BFPM). I then ask what this tells us about air resistance in the Angry Birds’ world, and my students see that it must mean the angry birds’s world has no drag forces. Nice!

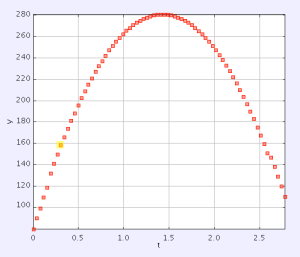
We then switch over to looking at the vertical motion. Starting with the y position:

The y position of the bird as a function of time.

My students see automatically that since the slope is not constant, the y-velocity must be changing. So we look at the y-velocity:

The y-veloctiy of the bird plotted against time.

Here students can see that the velocity graph shows constant accleration (CAPM), and this must mean the net force on the birds are constant and not zero. Could this be the gravitational force? We look at the evidence:

• The force is only vertical. Check.
• The force is constant. Check.
• The force causes an acceleration of . Hmm our acceleration isn’t this value, instead it is and I pause to see what units students can come up with. Pretty soon they see that the acceleration is 200 pixels per second for every second. How can we equate this to something in the real world? Well we can start by following Rhett’s lead and scaling the world by the height of the slingshot. If we do this using the ruler tool, we find 200 px=1.6 slighshots.

Now if we make the assumption that the angry birds world is the same as ours, it must be that:

Like Rhett, we found that the slingshot, and thus the angry birds are ridiculously huge. Which made my students ask, “What if the angry birds live on a really small planet, where they are normal sized, but the gravitational force is much less. Could this work?” Yes! I exclaim. (Note that they asked this without having studied the gravitational force in any detail, yet). We could study that too (marks idea journal: Angry Birds on Phobos).

In about 30 minutes of discussion, my students “discovered” the two big ideas of projectile motion: the horizontal component of motion is constant velocity, while the vertical component is constant acceleration. Both of these ideas are so well understood that my students were able to say they already thought they could solve most problems with these concepts. I told my students we’d take some time to practice, but essentially, in terms of understanding new ideas, they are ready to take a test on that unit now.

The key follow up that we didn’t have time to do just then would be to film and track the motion ball of a soccer ball thrown on a field or in our classroom and see if it matched the motion of the Angry Bird.